A science professor told BH that with espresso, “in technical terms you have Forchheimer flows instead of good old Darcy flows”. What’s that? Keen readers of this series will remember Darcy’s Law from our discussion of bed depth in espresso. Darcy’s Law is an equation normally used to predict things like the flow of water through an aquifer, or of oil seeping through the bedrock in an oilfield.

Applying Darcy’s Law to espresso making tells us why using more coffee slows the flow rate through the puck — the water has more distance to travel, which increases the effect of the resistance of the puck. However, things are never that simple.

Henry Darcy worked out his equation in the mid-19th century by measuring the flow of water through a column of sand, and his results only apply to this kind of slow flow. The faster flow through an espresso puck behaves slightly differently, and to understand why, we need to look in more detail at Darcy’s Law and what assumptions it makes.

What Is Darcy’s Law?

Darcy’s Law is an equation that predicts the flow rate of a liquid through a column of porous material.

• Permeability is a measure of how easily liquid passes through something — for example, gravel is more permeable than fine sand.
• Area is the cross-sectional area of the column
• The pressure difference across the column might come from gravity, or in the case of espresso, from our pump
• Viscosity is the ‘thickness’ of a liquid, or how it resists flow
• Length is the length of the column the liquid has to pass through

This equation shows us that making the column twice as wide allows twice as much water to flow through, while making it twice as long halves the flow rate. Doubling the pressure should also double the flow rate — but we know that in espresso this doesn’t happen — so why does Darcy’s Law break down in this case?

Reynolds Number

Darcy’s Law is only valid for slow flow, where the flow is mostly laminar — in other words where water molecules pass through in straight lines, rather than creating turbulence that interferes with the flow.

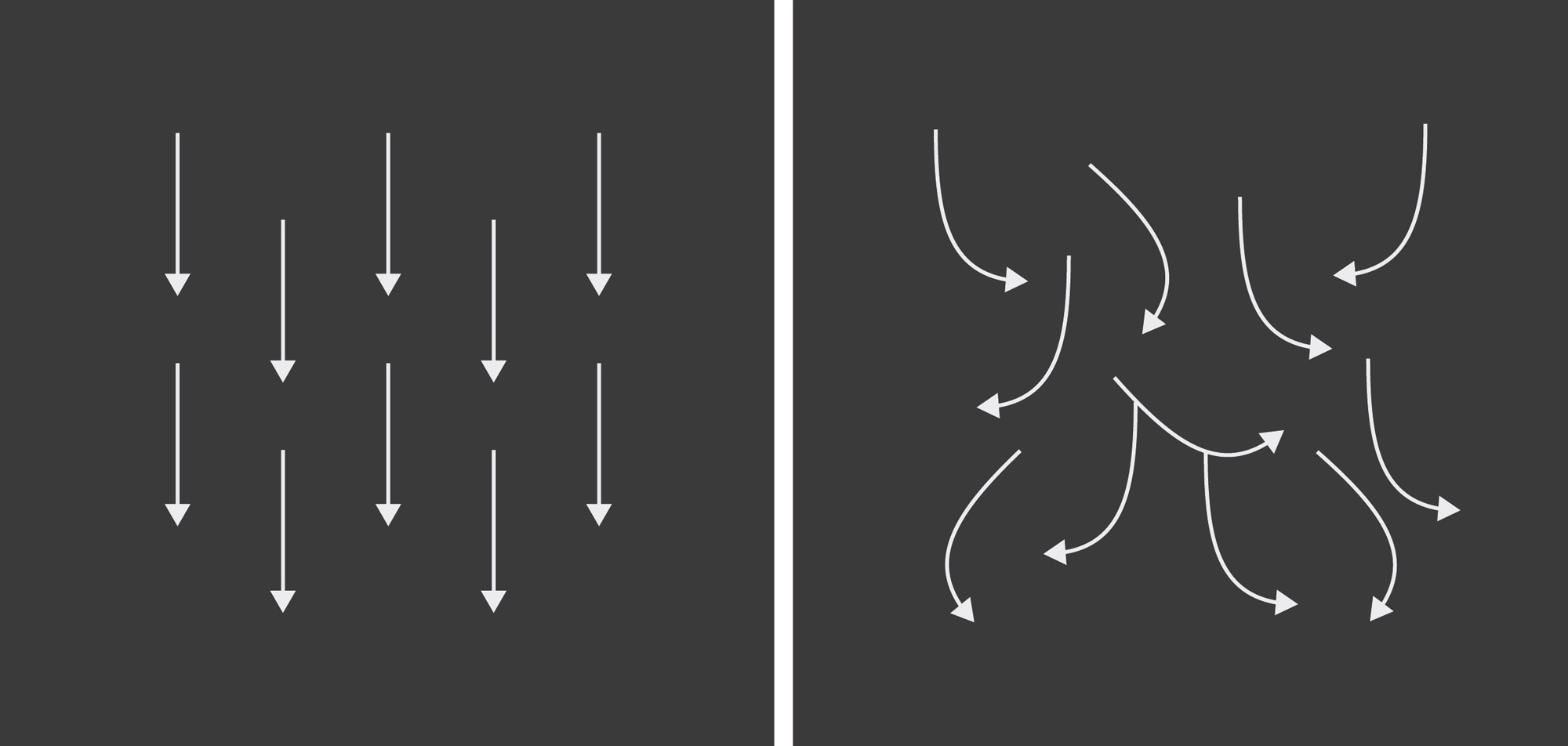Left: laminar flow / right: turbulent flow.

The Reynolds number is a measure that predicts if flow in a liquid will be laminar or turbulent — higher numbers indicate a higher likelihood of turbulent flow. Less viscous and faster moving liquids have higher Reynolds numbers — so water flowing quickly through an espresso puck has a higher Reynolds number than oil seeping through bedrock.

At Reynolds numbers above 10, the turbulence becomes significant enough that Darcy’s Law is no longer accurate. When this happens, we need to introduce a correction to the equation — known as the Forchheimer term.

The Darcy-Forchheimer Law

About 50 years after Darcy derived his equation, Forchheimer refined it by adding an additional term to account for the effect of turbulence. (Forchheimer, 1901) This term extends the equation and allows it to work at high flow rates. (J-Q Zhou et al, 2019).

The turbulence at high flow rates creates resistance, which means more pressure is needed to achieve a given flow rate. The Forchheimer term is thus a correction factor, which calculates the extra pressure needed to achieve a certain flow rate when the flow is turbulent.

The size of the term increases with the square of the flow rate, which means that to double the flow rate, the extra pressure required due to turbulence quadruples — so the faster the flow, the more important this factor becomes. Why exactly this happens, however, is still the subject of some debate and active research. (M Agnaou et al, 2017)

What Happens at High Pressure?

Even with Forchheimer’s correction, the equation still predicts that increasing pressure will increase flow. However, in espresso this is not the case — beyond a certain point, increasing pressure actually decreases flow, due to the puck compacting. (Rao, 2013) However, it seems the Darcy-Forchheimer Law could still apply in these conditions.

In Darcy’s terms, what’s happening here is that the increased pressure is reducing the permeability of the bed, by compacting the puck and thus reducing the size of the gaps or pores between the particles. This effect has been observed in rock or soil deep in the earth, that is compacted by the weight of the material above it — this effect is called confining pressure.

Darcy’s Law and its derivatives are still used as the basis for modelling flow in espresso, over 150 years after it was first proposed. (A Fasano and F Talamucci, 2000). Since extraction changes both the viscosity of the liquid, as it becomes espresso, and the permeability of the medium, as the puck breaks down, however, these equations can only ever tell one part of the story.

References

M Agnaou, D Lasseux, A Ahmadi, 2017. Origin of the inertial deviation from Darcy’s law: An investigation from a microscopic flow analysis on two-dimensional model structures. https://doi.org/10.1103/PhysRevE.96.043105

PH Forchheimer, 1901. Wasserbewegung durch Boden. Zeitschrift Verein Deutscher Ingenieure v. 45, n. 50, pp. 1781–1788.

S Rao, 2013. Chapter 3: Pump Pressure. In: Espresso Extraction: Measurement and Mastery

J‐Q Zhou, Y‐F Chen, L Wang, MB Cardenas, 2019. Universal Relationship Between Viscous and Inertial Permeability of Geologic Porous Media. https://doi.org/10.1029/2018GL081413