Un professeur de sciences a déclaré à BH qu'avec l'espresso, « En termes techniques, vous avez des flux de Forchheimer au lieu des bons vieux flux de Darcy ». Qu'est ce que c'est? Les lecteurs passionnés de cette série se souviendront La loi de Darcy de notre discussion sur la profondeur du lit dans l’espresso. La loi de Darcy est une équation normalement utilisée pour prédire des choses comme l’écoulement de l’eau à travers un aquifère ou l’infiltration de pétrole à travers le substrat rocheux d’un champ pétrolifère.
Candidature La loi de Darcy à la préparation d'un expresso nous explique pourquoi l'utilisation de plus de café ralentit le débit à travers le palet — l'eau a plus de distance à parcourir, ce qui augmente l'effet du résistance de la palet. Pourtant, les choses ne sont jamais aussi simples.
Henry Darcy a élaboré son équation au milieu du XIXe siècle en mesurant le débit d'eau à travers une colonne de sable, et ses résultats ne s'appliquent qu'à ce type d'écoulement lent. Le débit plus rapide d'un expresso palet se comporte légèrement différemment, et pour comprendre pourquoi, nous devons examiner plus en détail La loi de Darcy et quelles hypothèses il fait.
Qu'est-ce que La loi de Darcy?
La loi de Darcy est une équation qui prédit le débit d'un liquide à travers une colonne de matériau poreux.
| Débit = | perméabilité x surface x différence de pression |
| viscosité x longueur |
- La perméabilité est une mesure de la facilité avec laquelle un liquide traverse quelque chose. Par exemple, le gravier est plus perméable que le sable fin.
- L'aire est l'aire de la section transversale de la colonne
- La différence de pression à travers la colonne peut provenir de la gravité ou, dans le cas d'un expresso, de notre pompe.
- Viscosité est « l'épaisseur » d'un liquide, ou comment il résiste à l'écoulement
- La longueur est la longueur de la colonne à travers laquelle le liquide doit passer
Cette équation nous montre que le fait de rendre la colonne deux fois plus large permet à deux fois plus d'eau de s'écouler, tandis que la rendre deux fois plus longue réduit de moitié le débit. Doubler la pression devrait également doubler le débit - mais nous savons que dans l'espresso, cela n'arrive pas - alors pourquoi La loi de Darcy tomber en panne dans ce cas ?
Le numéro de Reynold
La loi de Darcy n'est valable que pour les débits lents, où le débit est majoritairement laminaire — en d'autres termes, où l'eau molécules traverser en lignes droites, plutôt que de créer turbulence qui gêne le flux.
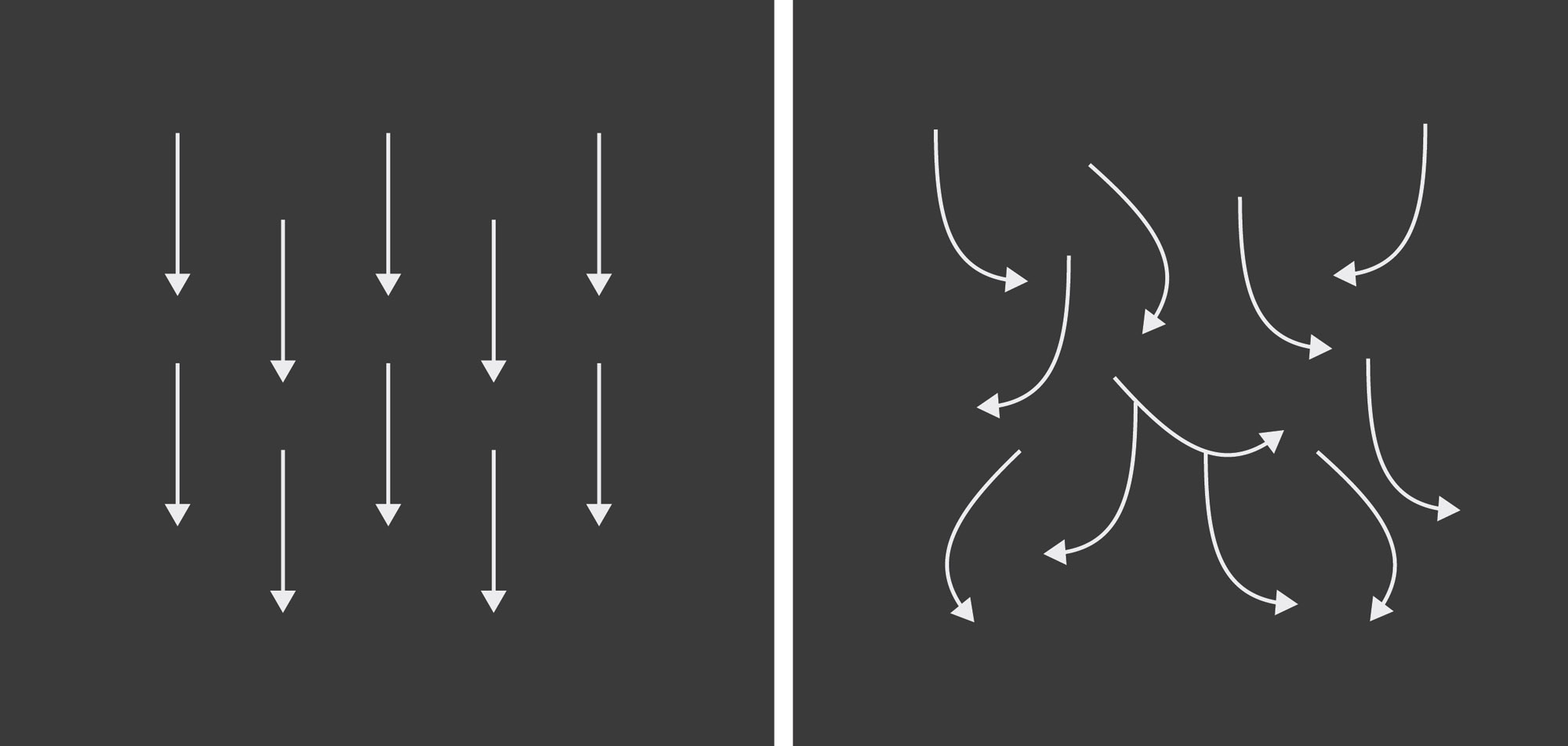 Gauche : écoulement laminaire / droite : écoulement turbulent.
Gauche : écoulement laminaire / droite : écoulement turbulent.
Le Le numéro de Reynold est une mesure qui prédit si l'écoulement dans un liquide sera laminaire ou turbulent – des nombres plus élevés indiquent une probabilité plus élevée d'écoulement turbulent. Les liquides moins visqueux et se déplaçant plus rapidement ont des nombres de Reynolds plus élevés - donc l'eau s'écoule rapidement dans un expresso palet a un nombre de Reynolds plus élevé que le pétrole qui s'infiltre à travers le substrat rocheux.
Aux nombres de Reynolds supérieurs à 10, le turbulence devient suffisamment important pour que La loi de Darcy n'est plus exacte. Lorsque cela se produit, nous devons introduire une correction à l’équation – connue sous le nom de Terme de Forchheimer.
La loi Darcy-Forchheimer
Environ 50 ans après que Darcy ait dérivé son équation, Forchheimer l'a affinée en ajoutant un terme supplémentaire pour rendre compte de l'effet de turbulence. (Forchheimer, 1901) Ce terme étend l'équation et lui permet de fonctionner à des débits élevés. (JQ Zhou et al, 2019).
Le turbulence à des débits élevés crée résistance, ce qui signifie qu’il faut plus de pression pour atteindre un débit donné. Le terme de Forchheimer est donc un facteur de correction, qui calcule la pression supplémentaire nécessaire pour atteindre un certain débit lorsque l'écoulement est turbulent.
La taille du terme augmente avec le carré du débit, ce qui signifie que pour doubler le débit, la pression supplémentaire nécessaire en raison de turbulence quadruple – donc plus le flux est rapide, plus ce facteur devient important. Cependant, la raison exacte pour laquelle cela se produit fait encore l’objet de débats et de recherches actives. (M Agnaou et al, 2017)
Que se passe-t-il à haute pression ?
Même avec la correction de Forchheimer, l'équation prédit toujours qu'une augmentation de la pression entraînera une augmentation du débit. Cependant, dans l'espresso, ce n'est pas le cas : au-delà d'un certain point, l'augmentation de la pression diminue en fait le débit, en raison de la palet compactage. (Rao, 2013) Il semble cependant que la loi Darcy-Forchheimer puisse encore s’appliquer dans ces conditions.
Selon Darcy, ce qui se passe ici, c'est que la pression accrue réduit la perméabilité du lit, en compactant le palet et réduisant ainsi la taille des espaces ou pores entre les particules. Cet effet a été observé dans la roche ou le sol profondément enfoui dans la terre, qui est compacté par le poids du matériau au-dessus – cet effet est appelé pression de confinement.
La loi de Darcy et ses dérivés sont toujours utilisés comme base pour modéliser le flux dans l'espresso, plus de 150 ans après sa première proposition. (A Fasano et F Talamucci, 2000). Puisque l’extraction modifie à la fois le viscosité du liquide, lorsqu'il devient expresso, et la perméabilité du milieu, comme le palet échoue, cependant, ces équations ne peuvent raconter qu’une partie de l’histoire.
Les références
M Agnaou, D Lasseux, A Ahmadi, 2017. Origine de la déviation inertielle de La loi de Darcy: Une enquête à partir d'une analyse microscopique d'écoulement sur des structures modèles bidimensionnelles. https://doi.org/10.1103/PhysRevE.96.043105
PH Forchheimer, 1901. Wasserbewegung durch Boden. Zeitschrift Verein Deutscher Ingenieure v.45, n. 50, pages 1781-1788.
S Rao, 2013. Chapitre 3 : Pression de la pompe. Dans : Extraction d'espresso : mesure et maîtrise
J‐Q Zhou, Y‐F Chen, L Wang, MB Cardenas, 2019. Relation universelle entre la perméabilité visqueuse et inertielle des milieux poreux géologiques. https://doi.org/10.1029/2018GL081413




J'ai adoré ce merveilleux article